Java刷题技巧

Mr.zh Lv3
  2024-04-01 21:50:32 2024-04-01 21:50:32 Created   2024-05-26 23:55:53 2024-05-26 23:55:53 Updated      8.2k Words  39 Mins  

刷题网站推荐

1
明确各个不同网站之间的区别：如力扣的代码是核心代码模式，而牛客等就是ACM模式，内容推荐系统刷力扣，针对练习洛谷、牛客中的难题，最后也可以多打打cf比赛

1.Arrays.sort自定义排序规则

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public int[][] reconstructQueue(int[][] people) {
       int n = people.length;
       List<int[]> list = new ArrayList<>();
       // 自定义二维数组的排序规则： 首先按照数组的第一个元素进行从大到小排序，如果相同，按照第二元素从小到大排序
       Arrays.sort(people , Comparator.comparingInt((int[] a )-> a[0]).reversed().thenComparing(
               (int[] a) -> a[1]
       ));

       Arrays.sort(people, (a , b) -> {
           if (a[0] == b[0]){
               return a[1] - b[1];
           }else{
               return b[0] - a[0];
           }
       });

       Arrays.sort(people , (a , b) -> {
           if (a[0] == b[0]){
               return a[1] - b[1];
           }else{
               return b[0] - a[0];
           }
       });
       for (int i = 0; i < people.length; i++) {
           System.out.println(people[i][0] + ":"+people[i][1]);
       }

       // 相当于此时已经按照身高排好序了，只需按照k进行插入即可
       for (int[] person : people) {
           list.add(person[1] , person);
       }

       return list.toArray(new int[people.length][]);
   }

2.大顶堆小顶堆的数组存储特点

1
2
1. 为简化计算，堆进行存储的时候数组下标也可从1开始，
公式就调整为：父节点=i/2，左子节点=i*2，右子节点=i*2+1（i是当前节点对应的数组下标）

例题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
代码答案如下：

import java.util.PriorityQueue;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        PriorityQueue<Integer> minQueue = new PriorityQueue<>((a,b)->a-b);



        int[] min = new int[n+1];
        for (int i = 0; i < n; i++) {
            minQueue.offer(in.nextInt());
        }
        // 需要注意的是，优先队列来建立堆进行存储，要使用这个方法，不能进行手动赋值
        Integer[] toArray = minQueue.toArray(new Integer[n]);

        int index = 1;
        for (Integer integer : toArray) {
            min[index++] = integer;
        }

      /**
         * 优先队列里面的元素：10
         * 优先队列里面的元素：23
         * 优先队列里面的元素：24
         * 优先队列里面的元素：26
         * 优先队列里面的元素：46
         */
        while (!minQueue.isEmpty()){
            System.out.println("优先队列里面的元素："+minQueue.poll());
        }


        /** 堆存储在数组中的结构为：
         * 堆在数组为：0
         * 堆在数组为：10
         * 堆在数组为：23
         * 堆在数组为：26
         * 堆在数组为：46
         * 堆在数组为：24
         */
        for (int i : min) {
            System.out.println("堆在数组为："+i);
        }
        in.nextLine();
        while (m-- > 0){
            // 接下来的m行，需要分别对每一行进行判断
            String str = in.nextLine();
            String[] strings = str.split("\\s");
            if (str.contains("is the root")){
                // 判断是不是头节点
                if (min[1] == Integer.parseInt(strings[0])){
                    System.out.println("T");
                }else {
                    System.out.println("F");
                }
            }else if (str.contains("are siblings")){
                int x = Integer.parseInt(strings[0]);
                int y = Integer.parseInt(strings[2]);
                int a = 0;
                int b = 0;
                for (int i = 1; i < n+1; i++) {
                    if (min[i] == x){
                        a = i;
                    }
                    if (min[i] == y){
                        b = i;
                    }
                }
                System.out.println(a/2 == b/2 ? "T" : "F");
            }else if (str.contains("is the parent of")){
                // 判断是不是父节点  -- 判断x是y的父节点
                int x = Integer.parseInt(strings[0]);
                int y = Integer.parseInt(strings[5]);
                for (int i = 1; i < n+1 ; i++) {
                    if (min[i] == y){
                        int f = i / 2;
                        if (min[f] == x){
                            System.out.println("T");
                        }else {
                            System.out.println("F");
                        }
                    }
                }

            }else {
                int x = Integer.parseInt(strings[0]);
                int y = Integer.parseInt(strings[5]);

                for (int i = 1; i < n+1; i++) {
                    if (min[i] == x){
                        int f = i / 2;
                        if (min[f] == y){
                            System.out.println("T");
                        }else {
                            System.out.println("F");
                        }
                    }
                }
            }
        }
    }
}

3. Java读取文件，暴力分割矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import java.io.*;
import java.util.Scanner;
public class Main {
    public static void main(String[] args) throws Exception {
        String path = "D:\\developer_tools\\idea\\java_code\\PTA\\src\\蓝桥杯\\day5\\data.txt";
        BufferedReader in = new BufferedReader(new FileReader(path));
        int[][] ints = new int[30][20];
        String line;
        int index = 0;
        while ((line = in.readLine()) != null){
            String[] strings = line.split(" ");
            for (int i = 0; i < strings.length; i++) {
                ints[index][i] = Integer.parseInt(strings[i]);
            }
            index++;
   //         按行读取，读取的每一行
//            System.out.println(line);
        }

        // 暴力破解，求出5行5列的子矩阵的最大值
        long res = Integer.MIN_VALUE;

        for (int i = 0; i <= ints.length - 5; i++) {
            for (int j = 0; j <= ints[0].length - 5; j++) {
                // 执行5次，从i 到后面5行
                // 从j 到后面 5 行
                long temp  = 0;
                for (int k = 0; k < 5; k++) {
                    for (int l = 0; l < 5; l++) {
                        temp += ints[k+i][l+j];
                        System.out.print(ints[k+i][l+j] +" ");
                    }
                    System.out.println();
                }
                res = Math.max(res , temp);
                System.out.println("第"+i + "行,第" + j+"列，构造结束");
            }
        }
        System.out.println(res);
       
    }
}

4. Java算法模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 求最大公约数模板
public int gcd(int a , int b ){
        int c = a % b;
        while (c != 0){
            a = b;
            b = c;
            c = a % b;
        }
        return b;
 }
// 求最小公倍数模板
int findLCM(int a , int b){
    return a * b / gcd(a , b);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 分解质因数模板 -- 将一个数分解成诺干质数相乘
static List<Integer> f(int n){
    List<Integer> res = new List<Integer>();
    for(int i = 2 ; i <= n ; i++){
        while(n % i == 0){
            res.add(i);
            n /= i;
        }
    }
    return res;
}
// 转化指定格式
static void factorization(int n ) {
		System.out.print(n+"=");
		for(int i = 2 ; i <= n ; i++) {
			while(n % i == 0) { // 表示当前的i可以被n整除，是他的倍数
				System.out.print(i);
				n /= i;
				if(n != 1) {  // 这个地方表示目前n不是最后一个
					// 表示不是最后一个
					System.out.print("*");
				}
			}
		}
	System.out.println();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
// 判断一个数是不是质数模板
static boolean f1(int num) {
		if(num <= 1) {    // 小于等于1的都不是质数
			return false;
		}
		for(int i = 2 ; i <= Math.sqrt(num) ; i++) {
			if (num % i == 0) {  // 表示存在了其他因数，肯定不是质数，返回即可
				// 质数定义是：只存在1或者他本身两个因数的数字，才属于质数
				return false;
			}
		}
		return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
// 快速幂
static double f2(int x , int y ) {
		double res  = 1;
		while (y != 0) {
			if(y % 2 == 1) {
				res *= x;
			}
			y >>= 1;
			x *= x;
		}
		return res;
 }

5. 回溯之切割问题

问题1 ： 力扣131. 分割回文串 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
代码如下：
	List<List<String>> res1 = new ArrayList<>();
    public List<List<String>> partition(String s) {
        if (s.length() == 0 || s == null) return res1;
        List<String> path = new ArrayList<>();
        backTracking(s , 0 , path);
        return res1;
    }

    private void backTracking(String s, int startIndex , List path ) {
        if (startIndex >= s.length()){
            res1.add(new ArrayList<>(path));
            return;
        }
        // 开始进行切割
        for (int i = startIndex; i < s.length(); i++) {
            if (f(s, startIndex , i )){
                // 表示这一段是回文串
                path.add(s.substring(startIndex , i+1));
                // 下一次的切割，从i当前执行的下一个开始切割哦
                backTracking(s , i + 1 , path);
                // 进行回溯
                path.remove(path.size()-1);
            }
        }
    }
    boolean f(String s , int start , int end){
        // 判断是不是回文串
        while (start <= end){
            if (s.charAt(start) != s.charAt(end)){
                return false;
            }
            start++;
            end--;
        }
        return true;
    }

问题2 力扣93. 复原 IP 地址 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
代码如下：
class Solution {
   List<String> res = new ArrayList<>();
    public List<String> restoreIpAddresses(String s) {
        if (s.length() > 12 ) return res;
        backTrack(s , 0 , 0);
        return res;
    }
//   使用了逗号的数量进行回溯的结束条件---- 这一点确实巧妙
    private void backTrack(String s, int startIndex, int pointNum) {
        if (pointNum == 3){
            if (isValid(s , startIndex , s.length() - 1)){
                res.add(s);
            }
            return;
        }
        for (int i = startIndex; i < s.length(); i++) {
            if (isValid(s , startIndex , i)){
                // 表示此时是一个合法的: 需要在i后面的位置添加一个.
                s = s.substring(0 , i + 1 ).concat(".").concat(s.substring(i+1));
                pointNum++;
                // 因为这个地方插入了一个逗号，所以下一个地方的是i+2
                backTrack(s , i+2,pointNum);
                // 下面两个地方是进行回溯的地方
                pointNum--;
                s = s.substring(0 , i+1).concat(s.substring(i+2));//回溯
            }else {
                break;
            }
        }
    }

    private boolean isValid(String s, int start, int end) {
        // 判断从start - end 两个边界都可以取到，是不是可以满足条件
        if (start > end){
            return false;
        }
        if (s.charAt(start) == '0' && start != end){
            // 表示此时这个字符长度不为1，但是他是零开头的，不合法，返回
            return false;
        }
 //    下面这个使用了累乘，来计算最终结果的访问大小
        
        int num = 0;
        for (int i = start; i <= end ; i++) {
            // 遇到非数字字符不合法，直接返回哦
            if (s.charAt(i) > '9' || s.charAt(i) < '0'){
                return false;
            }
            num = num * 10 + (s.charAt(i) - '0');
            if (num > 255){
                // 表示超过了数字的范围，直接返回哦
                return false;
            }
        }
        // 表示上面的条件都不是，此时就是一个合法的ip地址的字符串，从start到end
        return true;
    }
}

6. Java中快速读写的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import java.io.*;
import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
import java.util.Set;
public class Main_StreamTokenzier {
    static StreamTokenizer sc = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    // 注意点就是，每一次读取之前都要 sc.nextToken() 
    //  然后常用的只有两个方法，读取字符串和读取数字（默认double类型）两个方法
    public static void main(String[] args) throws IOException {
        sc.nextToken();
        int n = (int) sc.nval;
        int index = 1;
        for (int i = 0; i < n; i++) {
            set.clear();
            sc.nextToken();
            int k = (int) sc.nval;
            for (int j = 0; j < k; j++) {
                sc.nextToken();
                set.add((int)sc.nval);
            }
            map.put(index++ , new HashSet<>(set));
        }
//        for (Map.Entry<Integer, HashSet<Integer>> entry : map.entrySet()) {
//            System.out.println(entry.getKey()+":"+entry.getValue().toString());
//        }

    }
}

7. 指定字符数组长度转化为字符串

1
2
3
4
5
6
// String.valueOf(char[] chars , 0 , num) 这个方法的作用就是将chars字符数组，从chars[0]开始，取长度为num个元素，转化为字符串 	   
        char[] chars = new char[]{'a','b','c','d','e'};
        System.out.println(String.valueOf(chars , 0 , 2));
        System.out.println(String.valueOf(chars , 0 , 1));
        System.out.println(String.valueOf(chars , 0 , 3));
        System.out.println(String.valueOf(chars , 0 , 5));

8. KMP算法模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public class Main1 {
	public static void main(String[] args) {
		
		// 下面演示KMP算法 : 在s1中找到s2字符串首次出现的位置
		String s1 = "zhuzhuzhuhehehezhuhezhuhe";
		String s2 = "zhuhe";
		System.out.println(f_KMP(s1, s2));  // 6
		
	}
	static int f_KMP(String s1 , String s2) {
		int[] next = new int[s2.length()];
		getNext(s2 , next);
//		System.out.println(Arrays.toString(next));
		int j = 0;
		for (int i = 0; i < s1.length(); i++) {
			while (j > 0 && s1.charAt(i) != s2.charAt(j)) {
				j = next[j - 1];
			}
			if (s1.charAt(i) == s2.charAt(j)) {
				j++;
			}
			if (j == s2.length()) {
				// 这个地方表示s2已经全部匹配上了:返回下标即可
				return i - s2.length() + 1;
			}
		}
		// 匹配不上返回-1
		return -1;
		
	}
	// 求next数组，采用不减1的操作
	static void getNext(String s , int[] next) {
		next[0] = 0;
		int j = 0;
		for(int i = 1 ; i < next.length ; i++) {
			while(j > 0 && s.charAt(i) != s.charAt(j)) {
				// 如果找到不相同的，就看他的前一个
				j = next[j - 1];
			}
			if(s.charAt(i) == s.charAt(j)) {
				j++;
			}
			next[i] = j;
		}
	}
}

9. Java中大数的基本使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 加减乘除取模运算
System.out.println(BigInteger.valueOf(3).add(BigInteger.valueOf(2)));
System.out.println(BigInteger.valueOf(3).subtract(BigInteger.valueOf(2)));
System.out.println(BigInteger.valueOf(3).multiply(BigInteger.valueOf(2)));
System.out.println(BigInteger.valueOf(3).divide(BigInteger.valueOf(3)));
System.out.println(BigInteger.valueOf(14).mod(BigInteger.valueOf(3)));
// 案例--大数的阶乘
BigInteger res = BigInteger.ONE;	 
Scanner in=new Scanner(System.in);
 // 计算n的阶乘的方法     
int n=in.nextInt();
while(n != 0){
	res = res.multiply(BigInteger.valueOf(n));
	n--;
}
System.out.println(res);
// 进制转化内置方法
// 将一个数转化为2进制，8进制，16进制
System.out.println(Integer.toString(255 , 2));
System.out.println(Integer.toString(255 , 8));
System.out.println(Integer.toString(255 , 16));

// 将二进制，八进制 ， 16进制的字符串转化为十进制的方法
System.out.println(Integer.parseInt("11111111" , 2));
System.out.println(Integer.parseInt("11111111" , 8));
System.out.println(Integer.parseInt("11111111" , 16));

10 终要面对-Dijkstra算法

1
必要学会版 V1.0

GitHub源代码: https://github.com/yuanjiejiahui/Dijkstra

  1. 算法常用于处理单源出发到其他所有节点的最短路径问题，适用于不含有负权重的有向和无向图
  2. 算法采用贪心策略，具体代码借助堆来优化算法

力扣链接

相关博文 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
 	    List<int[]>[] g = new List[n];
        for (int i = 0; i < n; i++) {
            g[i] = new ArrayList<>();
        }
        // 构建图，使用list数组来进行构建哦
        for(int[] time : times){
            // 因为times数组中的下标从1开始的哦
            int u = time[0] - 1;
            int v = time[1] - 1;
            int w = time[2];
            g[u].add(new int[]{v , w});
        }
        final int INF = Integer.MAX_VALUE / 2; // 初始化dist数组需要使用哦
        // 一共n个节点哦
        int[] dist = new int[n];
        Arrays.fill(dist , INF);
        dist[k - 1] = 0; // 表示从当前节点到当前节点的最短路径为0，其他都为无限远
        PriorityQueue<int[]> pq = new PriorityQueue<>((a , b) -> a[0] - b[0]);
        pq.offer(new int[]{ 0 , k -  1}); //小顶堆，根据数组的第一个元素进行排序，用来记录从出发顶点，到达他所能到达的其他所有顶点的集合

        while (!pq.isEmpty()){
            // 每一次处理距离出发顶点最近的顶点哦
            int[] p = pq.poll();
            int currDist = p[0];
            int x = p[1];
            if (dist[x] < currDist){  // 表示此时不用更新dist[x]了
                // 表示此时dist[y] ，到达y的距离已经是最小值了，不需要进行处理
                continue;
            }
// 然后开始处理: g[y] 得到所有从y出发的顶点，能到达的下一个顶点，和他们的距离哦
            for(int[] e : g[x]){
                int y = e[0];// x到达的下一个顶点y
                int d = dist[x] + e[1];  // 经过x顶点到达y的路径距离
// 经过x和不经过x的两端距离进行比较，取出最小值即可
                if (d < dist[y]){  
                    dist[y] = d;
                    pq.offer(new int[]{d , y});
                }
            }
        }
        int res = 0;
        for (int i = 0; i < n; i++) {
            res = Math.max(res , dist[i]);
        }
        return res == INF ? -1 :res ;
    }
}

11 多次见面-并查集

附相关博文1 

1
我是不想见你的，奈何多次要见
  1. 题单1-寻找图中是否存在路径 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
class Solution {
    public boolean validPath(int n, int[][] edges, int source, int destination) {
        if(source == destination) return true;
        UF uf = new UF(n);
        for (int[] edge : edges) {
            uf.union(edge[0] , edge[1]);
        }
        // 总结： 并且集可以用来判断连通问题
        return uf.connected(source , destination);
    }
}

// 并查集
class UF{
    private int[] parent;
    private int[] sz; // 存储每个根节点所在组的数量个数
    int count ;  // 记录分组个数

    public UF(int n){
        this.count = n;
        this.parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
        this.sz = new int[n];
        for (int i = 0; i < n; i++) {
            sz[i] = 1;
        }
    }

    public boolean connected(int p , int q){
        // 判断pq是否在同一个组内
        return find(p) == find(q);
    }

    public int find(int p){

        // 查找p的父节点
        while (true){
            if (p == parent[p]){
                return p;
            }
            p = parent[p];
        }
    }

    public int getCount(){
        return this.count;
    }

    public void union(int p , int q){
        // 将这两个数组进行在一个组里面
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) return;
        // 现在不能简单的进行合并
//        parent[pRoot] = qRoot;
        if (sz[pRoot] < sz[qRoot]){
            // 将较小的合并到较大的上面
            parent[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        }else {
            // 此时qRoot较小，将较小的合并到大的上面
            parent[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
        //分组数量减减
        this.count--;
    }
}

  1. 题单2-547. 省份数量 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
class Solution {
    public int findCircleNum(int[][] isConnected) {
         int n = isConnected.length;
        UF uf = new UF(n);
        for (int i = 0; i < n; i++) {
            for (int j = i; j < n; j++) {
                // 表示直接连通哦
                if (isConnected[i][j] == 1){
                    uf.union(i , j);
                }
            }
        }
        // 省份的数量，其实就是最后的分组数量
        return uf.count;
    }
}


// 并查集
class UF{
    public boolean validPath(int n, int[][] edges, int source, int destination) {
        if(source == destination) return true;
        UF uf = new UF(n);
        for (int[] edge : edges) {
            uf.union(edge[0] , edge[1]);
        }
        return connected(source , destination);
    }

    private int[] parent;
    private int[] sz; // 存储每个根节点所在组的数量个数
    int count ;

    public UF(int n){
        this.count = n;
        this.parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
        this.sz = new int[n];
        for (int i = 0; i < n; i++) {
            sz[i] = 1;
        }
    }

    public boolean connected(int p , int q){
        // 判断pq是否在同一个组内
        return find(p) == find(q);
    }

    public int find(int p){

        // 查找p的父节点
        while (true){
            if (p == parent[p]){
                return p;
            }
            p = parent[p];
        }
    }

    public int getCount(){
        return this.count;
    }

    public void union(int p , int q){
        // 将这两个数组进行在一个组里面
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) return;

//        parent[pRoot] = qRoot;
        if (sz[pRoot] < sz[qRoot]){
            // 将较小的合并到较大的上面
            parent[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        }else {
            // 此时qRoot较小，将较小的合并到大的上面
            parent[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
        //分组数量减减
        this.count--;
    }
}
  1. 总结UF（并查集）模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

class UF{
    int[] parent ;
    int[] rank ; // 记录就是当前父节点他组内的个数
    int count ; // 记录目前一共有多少个分组数量
    public UF(int n){
        this.parent = new int[n];
        this.rank = new int[n];
        this.count = n;
        for (int i = 0; i < n; i++) {
            // 初始的情况下
            parent[i] = i;
            rank[i] = 1;
        }
    }
    public int find(int p){
        // 查找p节点的父节点
        while (true){
            if (parent[p] == p){
                return p;
            }
            p = parent[p];
        }
    }

    public boolean connected(int p , int q){
        int pRoot = find(p);
        int qRoot = find(q);
        return pRoot == qRoot;
    }

    public int getCount(){
        return this.count;
    }

    
    public void union(int p , int q){
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) return;  // 表示此时已经连通了，不需要在连通了
        
        // 进行连通操作： 优化步骤在于，将较短的树连接到较大的树上面
        if (rank[pRoot] < rank[qRoot]){
            parent[pRoot] = qRoot;
            rank[qRoot] += rank[pRoot];
        }else {
            parent[qRoot] = pRoot;
            rank[pRoot] += rank[qRoot];
        }
        
        // 因为此时将两个分组合并到一个分组上面了，故分组数量需要减减
        this.count --;
    }
}

4 . LCR 118. 冗余连接 

1
题目：在一个数中新添加了一条边，然后给你一个边的二维数组，请你求出，去掉哪一条边之后，仍然使得：剩余部分是一个有着 n 个节点的树（这一句话表示：删除一条边之后 ， n个节点仍然是连通的）。如果有多个答案，则返回数组 edges 中最后出现的边。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 代码如下
public int[] findRedundantConnection(int[][] edges) {
        int n = edges.length;
    //  UF类模板此处进行省略
        UF uf = new UF(n);
        for (int[] edge : edges) {
            // 题目中节点编号从1开始到n，故不要忘记减一
            int i = edge[0] - 1;
            int j = edge[1] - 1;
            if (uf.connected(i , j) == true){
                // 表示此时已经连接了
                return edge;
            }else {
                uf.union(i , j);
            }
        }
        return new int[0];
}

12 再见深搜

1
最优解不是使用dfs，为复习dfs，选择dfs

附上力扣题单 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
static int[][] direction = {{0 , 1} , {1 , 0} , {1,1}};
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;
        boolean[][] flag = new boolean[m][n];
        return dfs(matrix,0,0,target , flag);
    }
    public boolean dfs(int[][] matrix , int i , int j , int target , boolean[][] flag){
 // 先判断索引不合法，和已经访问过的，直接返回false
        if (i < 0 || i >= matrix.length || j < 0 || j >= matrix[0].length || flag[i][j]) {
            // 索引越界或已访问过，返回false
            return false;
        }
        // 主要这个逻辑来进行判断，是不是存在目标值
        if (matrix[i][j] == target) {
            return true;
        }
        flag[i][j] = true;
        for (int[] cur : direction) {
            int x = cur[0] + i;
            int y = cur[1] + j;

            // 如果存在true，表示找到了，返回true即可
            if (dfs(matrix, x, y, target, flag)) {
                // 如果在某个方向找到目标值，返回true
                return true;
            }
        }
        // 走到这个地方表示所有的方向都访问过了，但是没有找到，返回false
        return false;
    }

13 龟兔赛跑算法–快慢指针的使用

参考文章 

1
2
3
4
Floyd判圈算法
			- 解决是否存在环的问题
			- 解决求环的入口的问题
			- 解决求环的长度的问题

141. 环形链表 判断是否存在环

1
2
3
4
5
6
7
8
9
10
11
12
public boolean hasCycle(ListNode head) {
     ListNode fast = head;
     ListNode slow = head;
     while(slow != null && fast.next != null){
         fast = fast.next.next;
         slow = slow.next;
         if(fast == slow){ //表示相遇了
             return true;
         }
     }
     return false;
 }

142. 环形链表 II 求环的起点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public ListNode detectCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        ListNode res = head;
        while (fast != null && fast.next != null){
            fast = fast.next.next;
            slow = slow.next;
            if (fast == slow) {
                // 此时表示存在环，并且他们相遇在环的某一位置上哦
                while (res != slow){
                    res = res.next;
                    slow = slow.next;
                }
                return res;
            }
        }
        // 走到这个地方表示不存在环
        return null;
    }

对于求环的长度问题暂未遇到。思路是：假设存在环，快慢指针第一次相遇的位置一定在环的某个位置上，然后让快指针不动，慢指针走一圈，引入一个变量计算长度，当慢指针与快指针再次相遇的时候，刚好为环的长度。

14 Java数学类的三个方法

1
一定要注意，题目中要求的数据范围：是四舍五入，还是什么
  1. **Math.ceil(double a)**：向上取整方法。返回大于或等于参数的最小整数。如果参数是正数，则返回大于或等于该参数的最小整数；如果参数是负数，则返回小于或等于该参数的最大整数。返回值类型为double。
  2. **Math.floor(double a)**：向下取整方法。返回小于或等于参数的最大整数。如果参数是正数，则返回不大于该参数的最大整数；如果参数是负数，则返回大于或等于该参数的最小整数。返回值类型为double。
  3. **Math.round(float a) 和 Math.round(double a)**：四舍五入方法。返回最接近参数的整数。对于float类型的参数，返回int类型的整数；对于double类型的参数，返回long类型的整数。这是标准的四舍五入操作，即如果待舍入数的小数部分大于等于0.5，则向上取整；如果小于0.5，则向下取整。

15 再学完美、完全二叉树

相关博文1 相关博文2

  1. 二叉树的性质
1
2
3
4
5
（1）若二叉树的层次从0开始，则在二叉树的第i层至多有2^i个结点(i>=0)。
（2）高度为k的二叉树最多有2^(k+1) - 1个结点(k>=-1)。 (空树的高度为-1)
	度：结点所拥有的子树个数称为结点的度(Degree)
	叶子（终端结点）：没有孩子的结点(也就是度为0的结点)称为叶子(Leaf)或终端结点
（3）对任何一棵二叉树，如果其叶子结点(度为0)数为m, 度为2的结点数为n, 则m = n + 1。
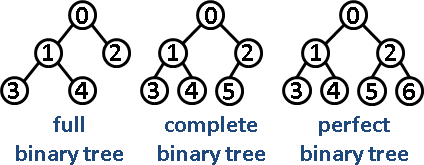
  1. 完美二叉树（满二叉树）
1
2
一个深度为k(>=-1)且有2^(k+1) - 1个结点的二叉树称为完美二叉树。 
(注： 国内的数据结构教材大多翻译为"满二叉树")。
  1. 完全二叉树
1
完全二叉树从根结点到倒数第二层满足完美二叉树，最后一层可以不完全填充，其叶子结点都靠左对齐。
  1. 完满二叉树
1
所有非叶子结点的度都是2。（只要你有孩子，你就必然是有两个孩子。）
  1. 完满(Full)二叉树 vs 完全(Complete)二叉树 vs 完美(Perfect)二叉树

题目 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// 代码如下
import java.util.Scanner;
public class Main {
    static int n , index = 1;
    static int[] nums , res;
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        nums = new int[n+1];
        res = new int[n+1];
        for (int i = 1; i <= n; i++) {
            nums[i] = in.nextInt();
        }
        dfs(1);
        StringBuilder ans = new StringBuilder();
        for (int i = 1; i < res.length; i++) {
            ans.append(res[i]+" ");
        }
        System.out.println(ans.toString().trim());
    }
    static void dfs(int i){
        if (i > n){
            return;
        }
        // 然后模拟后序遍历的顺序
        dfs(i * 2); // 左
        dfs(i * 2 + 1); // 右
        // 然后处理当前节点
        res[i] = nums[index++];
    }
}

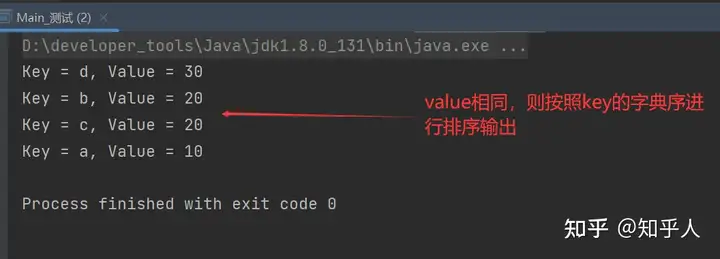
16 HashMap重写排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// HashMap 根据value进行排序
// 举例： 首先按照value进行从大到小的方式排序，然后如果value相同，则按照key从小到大排序

public class Main_测试 {
    public static void main(String[] args) {
        Map<String, Integer> hashMap = new HashMap<>();
        hashMap.put("b", 20);
        hashMap.put("a", 10);
        hashMap.put("c", 20);
        hashMap.put("d", 30);
        Set<Map.Entry<String, Integer>> entries = hashMap.entrySet();
        // 转换为列表
        List<Map.Entry<String, Integer>> list = new ArrayList<>(hashMap.entrySet());
        // 排序
        list.sort(new Comparator<Map.Entry<String, Integer>>() {
            @Override
            public int compare(Map.Entry<String, Integer> o1, Map.Entry<String, Integer> o2) {
                // 先比较value，如果value相同再比较key
                if (o2.getValue() - o1.getValue() != 0) {
                    return o2.getValue() - o1.getValue();
//                    return valueComparison;
                } else {
                    // value相同才按照key从小到大的方式进行排序
                    return o1.getKey().compareTo(o2.getKey()); // 从小到大排序
                }
            }
        });
        // 输出排序后的结果
        for (Map.Entry<String, Integer> entry : list) {
            System.out.println("Key = " + entry.getKey() + ", Value = " + entry.getValue());
        }
    }
}

17. 位移运算符

1
2
3
4
1. 左移m<<n 代表把数字m在无溢出的前提下乘以2的n次方。
2. 右移m>>n 代表把数字m除以2的n次方，原来是正数的还是正数，负数还是负数。注意，如果是单数，也就是二进制末位为1，则结果是将m除以2的n次方的整数商。

3. 记忆：小屁股指向谁，就向那边移动哦。

18. 无敌前缀树

1. 使用类的方式构建前缀树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
import java.util.HashMap;

public class Trie {
    class TrieNode {
        int pass ; // 表示经过这个节点的值
        int end; // 表示以这个节点结尾的值
        TrieNode[] nexts;
        // 当字符数量多的时候，数组不够使用，可以使用map来进行映射
        HashMap<Integer , TrieNode> map ;
        public TrieNode() {
            nexts = new TrieNode[26];
            map = new HashMap<>();
        }
    }
    private TrieNode root;
    public Trie() {
        this.root = new TrieNode();
    }
    // 将字符串word插入到前缀树中
    public void insert(String word){
        TrieNode node = root;
        node.pass ++ ;
        for (int i = 0 , path; i < word.length(); i++) {
            path = word.charAt(i) - 'a';
            if (node.nexts[path] == null){
                node.nexts[path] = new TrieNode();
            }
            node = node.nexts[path];
            node.pass++;
        }
        node.end++;
    }

    // 查询前缀树中，有多少单词以pre作为前缀
    public int countWordStartingWith(String pre){
        TrieNode node = root;
        for (int i = 0 , path ; i < pre.length(); i++) {
            path = pre.charAt(i) - 'a';
            if (node.nexts[path] == null){
                return 0;
            }
            node = node.nexts[path];
        }
        return node.pass;
    }

    // 查询前缀树中word单词出现了几次，求最后一个节点end即可
    public int countWordsEqualTo(String word){
        TrieNode node = root; // 从头节点进行出发
        for (int i = 0 , path ; i < word.length(); i++) {
            path = word.charAt(i) - 'a';
            if (node.nexts[path] == null){
                // 表示没有这个节点
                return 0;
            }
            node = node.nexts[path];
        }
        return node.end;
    }

    // 删除word单词在前缀树中构建：
        // 情况1 ： 如果之前word插入过前缀树，那么此时删掉一次
        // 情况2 ： 如果之前没有插入过前缀树，那么什么也不做
    public void erase(String word){
        if (countWordsEqualTo(word) > 0){
            TrieNode node = root;
            node.pass -- ;
            for (int i = 0 , path ; i < word.length(); i++) {
                path = word.charAt(i) - 'a';
                // 如果下一个节点减减之后为0，之后肯定都不用管了，直接删掉后面的即可，因为后面的此时都连接不上了
                if (--node.nexts[path].pass == 0){
                    node.nexts[path] = null;
                    return;
                }
                node = node.nexts[path];
            }
            // 走到最后将此时的end结束减减
            node.end -- ;
        }
    }
}
2. 使用静态变量的方式构建（推荐）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
static class Trie{
        static final int MAX = 150001;
        static int[][] tree = new int[MAX][26];
        static int[] pass = new int[MAX];
        static int[] end = new int[MAX];
        static int cnt ;
        public static void build(){
            cnt = 1;
        }
        // 将单词插入
        public static void insert(String word){
            int cur = 1;
            pass[cur]++;
            for (int i = 0 , path ; i < word.length(); i++) {
                path = word.charAt(i) - 'a';
                if (tree[cur][path] == 0){
                    tree[cur][path] = ++cnt;
                }
                cur = tree[cur][path];
                pass[cur]++;
            }
            end[cur]++;
        }
        // 然后统计每个单词在字典树中出现的次数即可
        public static int search(String word){
            int cur = 1;
            for (int i = 0 , path; i < word.length(); i++) {
                path = word.charAt(i) - 'a';
                if (tree[cur][path] == 0){
                    return 0;
                }
                cur = tree[cur][path];
            }
            return end[cur];
        }
        /**
         * 查找以这个字符串为前缀出现的次数 pass的值
         */
        public static int prefixNumber(String pre){
            int cur = 1;
            for (int i = 0 , path ; i < pre.length(); i++) {
                path = pre.charAt(i) - 'a';
                if (tree[cur][path] == 0){
                    // 表示断开了，不存在以他为前缀的哦
                    return 0;
                }
                cur = tree[cur][path];
            }
            return pass[cur];
        }
        /**
         * 删除
         */
        public static void delete(String word){
            if (search(word) > 0){
                // 存在才删除
                int cur = 1;
                pass[cur]--;
                for (int i = 0 , path ; i < word.length(); i++) {
                    path = word.charAt(i) - 'a';
                    if (--pass[tree[cur][path]] == 0){  // 这个地方每一次将pass已经进行自减过了哦
                        // 表示下一个是空
                        tree[cur][path] = 0;
                        return;
                    }
                    cur = tree[cur][path];
                }
                end[cur]--;
            }
        }

        public static  void clear() {
            for (int i = 1; i <= cnt ; i++) {
                Arrays.fill(tree[i] , 0);
                pass[i] = 0;
                end[i] = 0;
            }
        }
}
3. 相关题目讲解

LCR 062. 实现 Trie (前缀树) 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class Trie {

    // 使用静态数组的方式
    final int MAXN = 50001;
    int[][] tree = new int[MAXN][26];
    int[] pass = new int[MAXN];
    int[] end = new int[MAXN];
    int cnt ;

    public Trie() {
        cnt = 1;
    }

    public void insert(String word) {
        int cur = 1;
        pass[cur]++;
        for (int i = 0 , path ; i < word.length(); i++) {
            path = word.charAt(i) - 'a';
            if (tree[cur][path] == 0){
                // 表示此时这个没有路，构建出来即可
                tree[cur][path] = ++cnt;
            }
            cur = tree[cur][path];
            pass[cur]++;
        }
        end[cur]++;
    }

    public boolean search(String word) {
        int cur = 1;
        for (int i = 0 , path ; i < word.length(); i++) {
            path = word.charAt(i) - 'a';
            if (tree[cur][path] == 0){
                return false;
            }
            cur = tree[cur][path];
        }
        return end[cur] != 0 ? true : false;
    }

    public boolean startsWith(String prefix) {
        int cur = 1;
        for (int i = 0 , path ; i < prefix.length(); i++) {
            path = prefix.charAt(i) - 'a';
            if (tree[cur][path] == 0){
                return false;
            }
            cur = tree[cur][path];
            
        }
        return true;
    }
}

19 .数论

1
前言：真心感慨先人的智慧，各种定理，各种推理，全部给出结论，而我在几十年后的今天看了好久才能看出一丝门道，学无止境啊

1. 费马小定理

1
2
3
4
5
6
7
1. 概念：如果p是一个质数，而整数a不是p的倍数，即a与p互质，那么满足等式a^(p-1)≡1(mod p)，即a的(p-1)次方除以p的余数恒等于1
2. 推论：a mod p = 1 / a ^ (p-2)    =>     引出逆元计算
3. 逆元可以用来进行模算术除法，即除以一个数可以转化为乘以其逆元。
---------------------------------------------------------------------------------
综上所述：假如要求a在质数p下的逆元，即为 a ^ (p-2)  ，因为除以 a 等于除以1 / a ^ (p-2)
相当于乘以 a ^ (p-2) , 即正好满足逆元定义。（注意这个公式下p一定要是质数哦）

2. 快速求逆元

前提，p为质数

题目：

1
2
3
技巧1 ： 0 异或 任意数 等于 任意数
（异或运算中，不同为1 ，相同为0）
System.out.println(0 ^ 312312321);
  • 注意这个和快速幂还有些不同，在利用下述模板进行逆元求解的时候，不要忘记模m了
1
2
3
4
5
6
7
8
9
10
11
12
static long pow2(long x , long y , long m){
        long res = 1;
        while (y != 0){
            if (y % 2 == 1){
                // 表示此时是奇数
                res = res * x % m;
            }
            x = x * x % m;
            y = y/2;
        }
        return res;
}

  • 蓝桥真题

  • 给定质数模数 M=2146516019M=2146516019，根据费马小定理对于不是 MM 倍数的正整数 aa，有 a(M−1)≡1(mod M)a(M−1)≡1(mod M)，求出 [1,233333333][1,233333333] 内所有自然数的逆元。则所有逆元的异或和为多少？

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21

    - ```java
      long res = 0;
      long m = 2146516019;
      for (int i = 1; i <= 233333333 ; i++) {
      	res ^= pow2(i , m - 2 , m);
      }
      System.out.println(res);
      =============================================================================
       static long pow2(long x , long y , long m){
              long res = 1;
              while (y != 0){
                  if (y % 2 == 1){
                      // 表示此时是奇数
                      res = res * x % m;
                  }
                  y = y/2;
                  x = x * x % m;
              }
              return res;
      }

3. 数论

20 差分数组

1
对连续子数组的操作，可以转变为对差分数组中的两个数的操作

1. 定义和常用性质

1
2
3
4
5
6
7
8
9
10
11
# 定义：对于数组a,他的差分数组d为：
	d[0] = a[0] , d = 0
	d[i] = a[i] - a[i - 1] , d >= 1
# 性质：
    1.从左向右累加d中的元素，可以得到原数组a
    2.将子数组a的子数组a[i] , a[i+1] ...  a[j] 都加上x 等价于：
    			   将d[i] 增加x , 将 d[j+1] 减少 x
# 说明：
	利用性质2，可以实现在O(1)的时间复杂度下完成对a的子数组的操作，然后利用性质1还原数组
# 注意点：

2. 例题

1094. 拼车 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public boolean carPooling(int[][] trips, int capacity) {
     // 0 <= fromi < toi <= 1000
        // 定义a[i] 表示到底位置 i 的时候 车上的人数，需要判断所有的a[i] 是否满足 <= capacity
        int[] d = new int[1001];

        for (int[] trip : trips) {
            int num = trip[0] , start = trip[1] , end = trip[2];
            // start 到  end - 1  是增加上: 刚好满足差分
            // end 是减少人
            d[start] += num;
            d[end] -= num;
        }
        int s = 0;
        for (int i : d) {
            s += i ;
            if (s > capacity){
                return false;
            }
        }
        return true;
    }
}
  • Title: Java刷题技巧
  • Author: Mr.zh
  • Created at : 2024-04-01 21:50:32
  • Updated at : 2024-05-26 23:55:53
  • Link: https://redefine.ohevan.com/2024/04/01/Java刷题技术/
  • License: This work is licensed under CC BY-NC-SA 4.0.
On this page
Java刷题技巧
  1. 1.Arrays.sort自定义排序规则
  2. 2.大顶堆小顶堆的数组存储特点
  3. 3. Java读取文件，暴力分割矩阵
  4. 4. Java算法模板
  5. 5. 回溯之切割问题
  6. 6. Java中快速读写的代码
  7. 7. 指定字符数组长度转化为字符串
  8. 8. KMP算法模板
  9. 9. Java中大数的基本使用
  10. 10 终要面对-Dijkstra算法
  11. 11 多次见面-并查集
  12. 12 再见深搜
  13. 13 龟兔赛跑算法–快慢指针的使用
  14. 14 Java数学类的三个方法
  15. 15 再学完美、完全二叉树
  16. 16 HashMap重写排序
  17. 17. 位移运算符
  18. 18. 无敌前缀树
  19. 19 .数论
  20. 20 差分数组